Lorenz - Transformation - ergänzende Notiz zum Buch von Max Born
Miroslav J. Dvorecky
Zum Zeitpunkt der Entstehung der Einsteinschen Relativitätstheorie waren die Erkenntnisse in der Physik über Aufbau der Materie sehr fortgeschritten:
- In der Umgebung eines elktrisch-geladenen Körpers war keine Existens eines magnetischen Feldes erkennbar. Erst durch Energieanwendung die eine Bewegung
des geladenen Körpers zur Folge hatte, entsatnd plötzlich ein magnetisches Feld zusätzlich zum vorhandenen elektrischen Feld. Eine Analogie zur Trägheit der Masse war ersichtlich,
wie auch der Zusammenhang der Energie und der Masse. Eine elektrisch ungeladene Masse kann man also mit weniger Energie in Bewegung setzen, weil zur Erzeugung des magnetischen Feldes kiene
gebraucht wird. Genauere Messungen der Radioktiven Beta-Strahlen bestätigten den Zusammenhang von Geschwindigkeit und der Masse der emittierten Elektronen.
Mit der steigenden Geschwindigkeit eines Elektrons steigt auch der Bedarf der notwendigen Energie für die Steigerung seiner Geschwindigkeit, weil seine Masse zugenommen hat. Die Existenz der angenommenen Masse
( Messungen von Kaufmann, 1901 ) schien nicht notwendig zu sein, als Masse war es möglich nur die Energie in Betracht zu nehmen.
- H.A.Lorenz erklärte in seiner Hypothese (1904) die Längenschrumpfung eines bewegten Körpers in seiner Bewegungsrichtung ( als Einwirkung des Äthers ).
- Die Gravitation war weiterhin Abseits der Erkenntnisse über das elektromagnetische Feld. Die Existens von gewissem Äther beherschte die Physik so wie heute die Existens von
dunkler Energie.
- Michelson und Morley haben bewiesen, dass die Lichtgeschwindigkeit sich nicht erhöhen lässt. Sie haben aber nur die durchschittliche Geschwindigkeit gemessen.
- Lorenz berechnete elektromagnetische Abläufe in bewegten Systemen und verglich sie mit Abläufen im hypothischen Äther. Er kam zum Schluss, dass man verschiedene Zeiten
für diese Systeme einführen muss ("Ortzeiten") und stellte die Zeit-Umrechnungen ( Transformationen ) in Gleichungen auf. Gleichzeitig beschreibt seine Theorie die Unmöglichkeit
die absolute Bewegung zum newtonschen absoluten Raum oder den Äther für Beobachter in verschiedenen bewegten Systemen festzustellen. Nur relative Beziehungen sind danach erkennbar
( Einen Messbaren Orientierungspunkt im Absoluten Raum hat niemand feststellen können. Das gleiche gilt für den Äther ).
- Das elektromagnetische Feld, definiert durch die Maxwelsche Feldgleichungen, messbar, berechenbar, tritt jetzt für den Äther ein. Lorenz aber tut sich schwer den Äther aufzugeben,
obwohl er und der Poincaré hervorgeragende Ergebnisse bei der Unterschung der Elektrodynamik ausgearbeitet haben. Poincaré rückte schließlich doch von dem Stanpunkt von Lorenz ab.
Das die Gleichgültigkeit der unendlich vieler Systeme eine Gültigkeit des Relativitätsprinzips darstellte, wusste er. Er hat die Folgen dieser Annahme aber nicht manifestiert.
- Einstein ( 1905 ) rückte von der Annahme eines absoluten Raums und absoluter, dauernder Zeit Newton´s ab, sowie Annahme eines Äthers, und in seine Theorie übernahm er die Gravitation,
die elektromagntische Dynamik, die Zeitrelativität und die absolute Lichtgeschwindigkeit c, die in allen Systemen gleich ( inert ) ist .
Die Wirkung der Gravitation:
Starkes Gravitationsfeld verlangsamt die Interaktivität der Massenteilchen die zusätzlich auf sie als fremde Kraft einwirkt. Auch biologische Abläufe werden verlangsamt.
Vorstellen kann man es sich, wenn man irgendeine Massenteilchen betrachtet, die sich in einem Medium bewegen und aufeinander durch eigene Kräfte wirken, ( Gasmoleküle ).
Falls eine zusätzliche Kraft ( Gravitation ) an sie beginnt zu wirken, müssen sie ihre Energie mit dieser teilen. Eine Uhr in einer Mine läuft deswegen langsamer als eine
an der Oberfläche.
Die Wirkung der Geschwindigkeit:
Wenn ein Stern explodiert, verbreitet sich das Ereignis als Information in allen Richtungen mit der Lichtgeschwindigkeit c. Eine graphische Darstellung aller Zustände solches
Ereignisses ist nicht einfach. Eine bildliche Darstellung der Ergebnisse der Relativitätstheorie ist wesentlich komplexer ( vierdimensionale Vektoren in Tensormatrix ) und deshalb leider unmöglich. Aus diesem Grund beschränken wir uns
nur auf zweidimensionale Graphik um die prinzipielle Darstellung der zeitlichen Abläufe in einem Denkversuch zu zeigen.
In Teilchenbeschleunigern erfahren radioaktive Atome Verlangsamung des eigenen Zerfalls, weil ihre eigene Zeit bei fast Lichtgeschwindigkeit langsamer abläuft.
Wenn sich zwei Teilchen gegeneinander bewegen mit gleichen Geschwindigkeiten zum Bsp. v1 = c/1,5, und v2 = c/1,5, dann müsste mathematisch die Zusammenstoss-Geschwindigkeit ( Summe = 1,3 c ) die Lichtgeschwindigkeit c übersteigen.
Verwendete Begriffe:
c Lichtgeschwindigkeit, Konstante
t Zeit, Variable
c.t Strecke, die das Licht in der Zeit t zurücklegt
v Geschwindigkeit, mit der ein System S´ mit den Koordinaten x´, y´ sich bewegt
v.t Strecke, die ein System in Bewegung in der Zeit t zurücklegt
S Ein ruhendes System mit den Koordinaten x, y
S´ Ein in Bewegung sich befindendes System mit den Koordinaten x´, y´
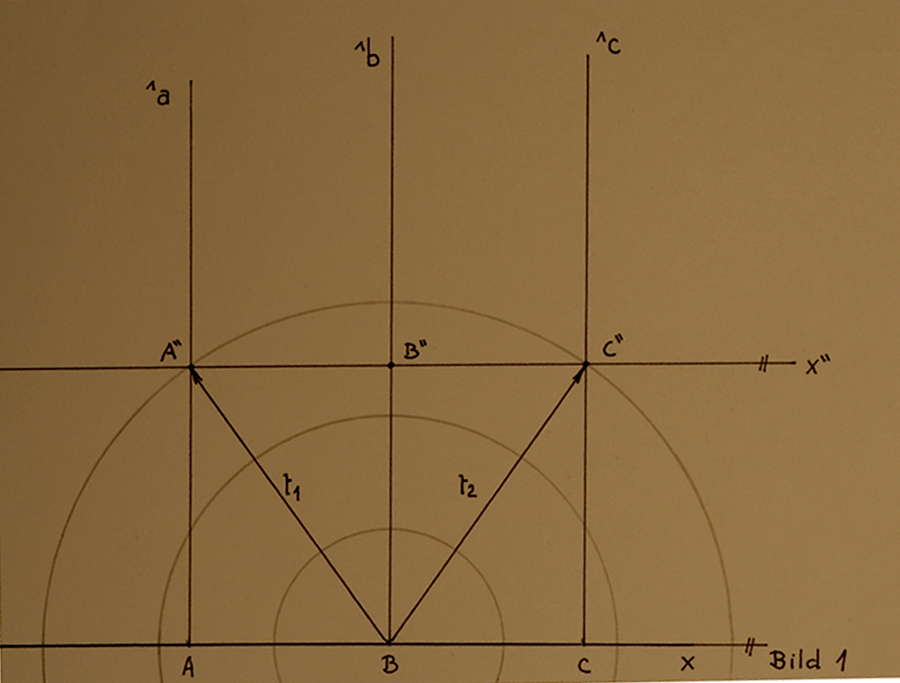
In dem folgenden Bild ist ein ruhendes System S mit den Koordinaten x, und y = ct dargestellt. An der Achse x befinden sich in gleichen Abständen drei Punkte A,B und C.
In dem Punkt B befindet sich eine Lichtquelle, dessen Photonen ( Lichtwellen als Kreise dargestellt ), die Punkte A" und B" gleichzeitig erreichen ( t1 = t2 ).
Ein Beobachter der sich im System S befindet, oder ein anderer der ausserhalb des Systems verweilt, sieht die Lichtquelle B in der Mitte zwischen den Punkten A und C.
Die Gerade x", die die Punkte A" ↔ C" verbindet, liegt in dem Koordinatensystem S parallel zur Achse x. Die Linien ^a und ^c kann man sich auch als Lichtstrahlen vorstellen.
Die beschriebenen statischen Beziehungen ändern sich beim dynamischen Prozess, für einen Beobachter der sich ausserhalb des Systems befindet, und ein System der in Bewegung ist beobachtet.
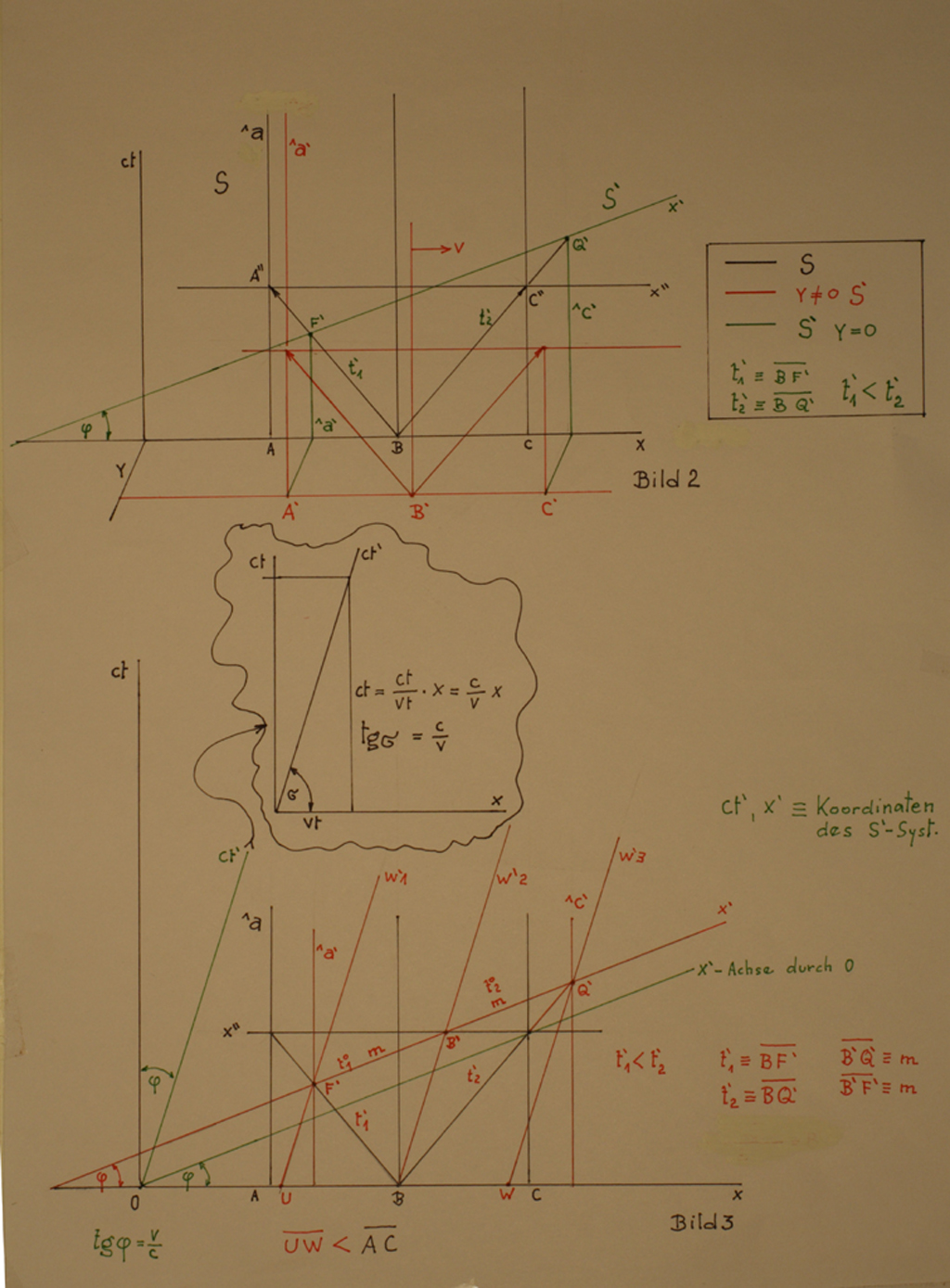
Das Bild 2 ist Ergänzung des Bildes 1 in dem Sinn, dass zwei gleiche Systeme zuerst in Ruhe verweilen und sich dadurch im Koordinatensystem decken, ( y = 0 ).
Nur zur Veranschaulichung ist das im Vordergrund stehende System rot gezeichnet und an der y-Achse nach vorne versetzt. Wird die Versetzung aufgehoben ( y=0 ), dann werden die
grünen Linien gültig.
Falls zum gewissen Zeitpunkt das im Vordergrund sich befinndende System S´( rot ) mit konstanter Geschwindigkeit v in Bewegung entlang der Achse x gesetzt wird,
wird der ruhende Beobachter im System S ( schwarz ) folgendes messen:
( Das System in Bewegung bezeichnen wir S´. Auch dem System zugehörige Elemente werden wir mit Strich kennzeichnen ):
Der Punkt B´ befindet sich in der Mitte des Systems S´ und zwei gleichzeitig ausgestrahlten Photonen aus der Quelle B´ sind auf dem Weg zu Punkten F´und Q´.
In der Zeit in der die Photonen unterwegs sind, sieht der ruhende Beobachter dass sich die Linie ^a' ( "Weltlinie" ) dem linken Photon mit der Geschwindigkeit v entgegen nähert, während die Linie ^c' dem rechten Photon davonläuft.
Für den Beobachter ist also die Zeit t´1 kürzer als die Zeit t´2 und diese Tatsache entspricht seiner Messung. Aber ein Beobachter der im System S´ veweilt und aus seiner Lichtquelle B´ laufende Photonen beobachtet, merkt keinen zeitlichen Unterschied,
er misst t´1=t´2 und merkt gar nicht das er, und das System S´ sich in Bewegung befinden.
( Die Lichtgeschwindigkeit in beiden Systemen ist die gleiche. Die Austronauten in einem Satelitenlabor müssen sich die Erde ansehen um ihre Bewegung zu erfahren, und ihre Messungen verlaufen ohne Unterschied, also wie auf der Erde ).
Im Bild 3 sind die Schnittpunkte F´und Q´ mit den Linien ^a' und ^c' durch die Gerade x´ verbunden. Der ruhende Beobachter im System S sieht auch die Lichtquelle B´ in der Mitte der Linie F´↔ Q´.
Durch Verbindung der Punkte B und B´ gewinnen wir die Weltlinie w'2 die geneigt ist. Die übrigen Weltlinien die durch die Punkte F´und Q´ führen, müssen zur Weltlinie w'2 parallel verlaufen.
Am Bild 3 schneiden diese Weltlinien die x-Achse in den Punkten U und W. Die Länge U↔W ist kürzer als die Länge A↔C . Das bedeutet, dass der ruhender Beobachter die Länge A´↔C´ als verkürzt sieht.
( Ein Koordinatensystem muss nicht rechtwinklig sein. Eine exakte Transformstion aus einem System in ein anderes ist gegeben. Die Abhängigkeit der Längen-Schrumpfung von der Geschwindigkeit war 20 Jahre vor Einstein bekannt.)
Die Neigung der x´-Achse zur x-Achse findet physikalisch nicht statt, sie entsteht nur in der graphischen Darstellung. Die mathematische Formulierung ergibt auch einen Neigungswinkel der x´-Gerade.
Die Achse ct´ lassen wir durch den Nullpunkt verlaufen und stellen wir für sie die Gleichung einer Gerade auf. ct´ soll beliebigen Punkt auf der ct´-Achse darstellen.
Im ruhenden System S hat die Lage des Punktes ct´ den Wert ct auf der ct-Achse. Die Neigung der ct´-Achse ( Winkel σ) bestimmt die durch den Nullpunkt verlaufende Gerade
ct= tgσ. x = (ct / vt) . x = (c/v) . x ( alle Punkte auf der ct´-Achse sind gleich ct im S-System , ein Punkt ct´ hat die Koordinaten
im System S, ( ct, x ).
(1) x = (v/c) . ct ( das x ist den Werten an der Achse ct´ zugeordnet )
x´= 0 ( Gleichung der ct´-Achse )
Die Neigung der ct´-Achse ist tgσ= c/v
Die Achse x´ muss bestimmt werden.
Durch Beobachtung = Messung des Zusammenhangs der Ereignisse in einem bewegten System zum ruhenden System, werden Erkentnisse gewonnen. So ist der Ausdruck "der Beobachter sieht"
mit dem Asdruck "die Geräte des Beobachters zeigen an", gleich zu setzen.
Gleichung der x´-Achse ist ct´= 0
So einfach wie es war die Gerade ct´ zu beschreiben, ist es für die x´-Achse nicht. Die Bewegung des Systems S´entlang der x-Achse bedarf relativistische Beziehungen.
Der ruhende Beobachter im System S sieht die Mitte B´ zwischen den Punkten F´↔ Q´ im bewegten Systen S´. Seiner Überlegung nach ( die Neigung der Gerade x´ sieht er nicht ) müsste eine Lichtquelle in B´ die
zwei Photonen gleichzeitig in Gegenrichtungen auf der Achse x´ aussendet, eine Zeitdifferenz für beide Photonen ergeben, derer Ursache in der Geschwindigkeit des Systems S´ liegt.
Dem nach müsste das linke Photon den Punkt F´schneller erreichen als das rechte Photon den Punkt Q´. Er nimmt also den Bezug auf die Messung der Zeitdifferenz zwischen dem linken und dem rechten Photon
aus der Sicht des Beobachters im System S und des Punktes B.
Die Gerade F´↔ Q´ ist im Punkt B´ geteilt auf die 2 gleichen Längen m. Das linke Photon erreicht den Punkt F´ in kürzerer Zeit wegen der Summe der Geschwindigkeiten (v+c) .
Das rechte Photon erreicht den Punkt Q´ verspätet wegen der Geschwindigkeitendifferenz, als wäre seine Geschwindigkeit um v gedrosselt. Die Strecke m geteilt durch
die Summe der Geschwindigkeiten bestimmt die Laufzeit des Photons:
t°1= m / (v+c) t°2 = m / (c-v) ( Die Bezeichnung der Teilzeiten ist leicht unterschiedlich: t´1 ist nicht gleich t°1 )
Die Differenzzeit für die Strecken m erhalten wir durch Subtraktion von t°2 und t°1 [ t°2 = m/(c-v) ist größer als t°1 = m/(c+v) ]
(2) δt´ = m / (c-v) - m / (c+v) = [m . (c+v) - m (c-v)] / (c+v) . (c-v) = m .(c+v-c+v) / (c²-v²) = 2vm / (c²-v²).
Ein Photon das die Bahn von dem Punkt F´ zum Punkt Q´ mit der Lichtgeschwindigkeit zurücklegt, bewältigt die Strecke δx´ = c.t´ = c.( t°1 + t°2 )
(3) δx´ = [ m/(c+v) + m/(c-v) ] . c = 2mc²/ (c² - v²)
Die Differenzgeschwindigkeit ist gegeben durch
δx´ / δt´ = 2mc² / 2mv = c² / v und daraus folgt die Gleichung von grungsätzlicher Bedeutung
(4) δx´ = (c²/v) . δt´ = c/v . c.δt´
Die Neigung der x´-Achse ist:
(5) tgφ = v/c ( v/c = β Hauptelement des Lorenz-Faktors ). ( Für den Fall v = c wird tgφ = 1 ---> φ = 45°, Grenze des Minkovskis Ereignishorizonts )
Notiz:
Für Intensität des Elektrischen Feldes E und der Intensität des zugehörigen magnetischen Feldes H in einer Umgebung mit magnetischer Permeabiltät µ gilt ( Experiment von Faraday ):
E = (v/c) µ H ( Bewegter Draht im mag. Feld ). Dieser Faktor war dem H.Lorenz aus der Maxwellschen Überlegungen bekannt.
______________________________________________________________________________________________________________________________________________________________________________________
Setzen wir die Anfangspunkte der Koordinatensysteme S und S´ in gemeinsamen Nullpunkt.
In dem ruhenden System S werden wir einen Punkt P betrachten, der die Koordinaten im System S P(x,ct) hat.
Ein mit der Geschwindigkeit v entlang der x-Achse sich bewegendes System S´ hat für den Punkt P die Koordinaten ( x´, ct´ ).
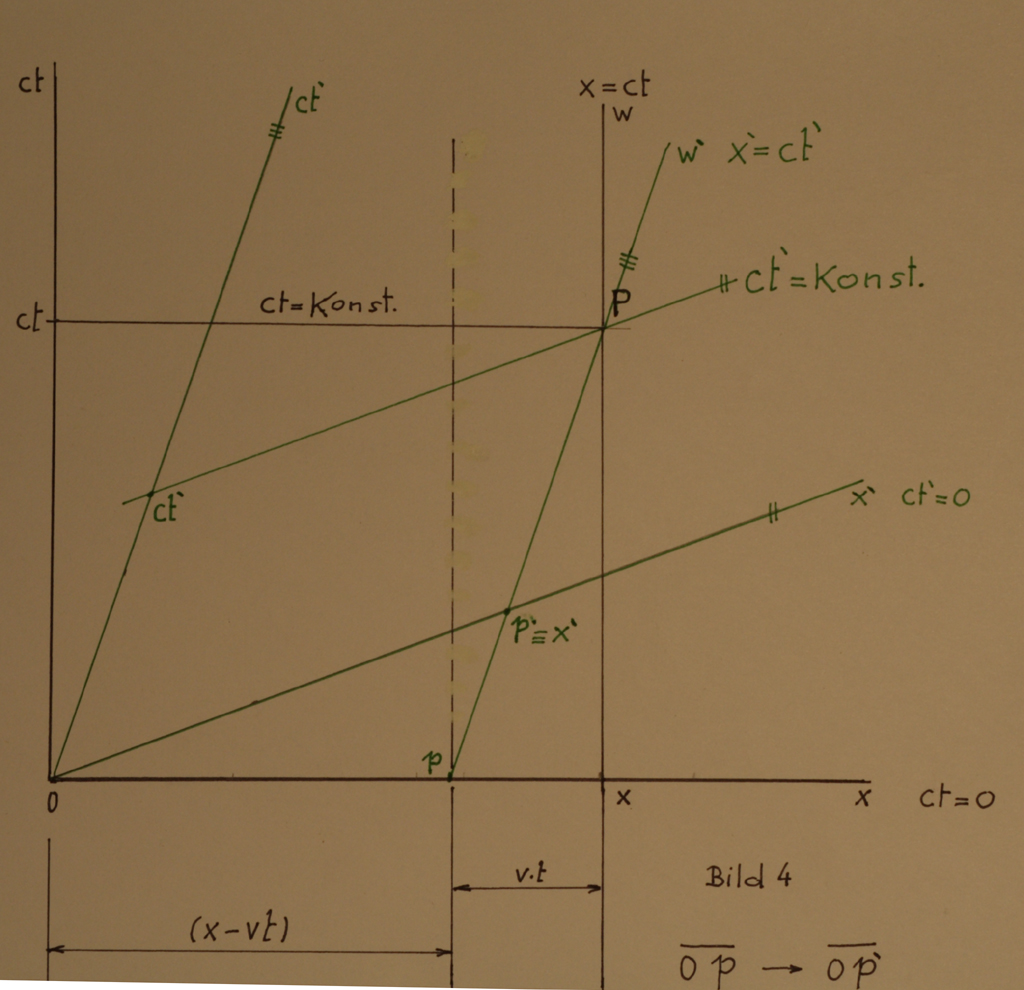
Die Länge 0↔p wird in das bewegte System als Länge 0↔p´ transformiert, wie es im Bild 4 eingezeichnet ist.
Gemäß der vorherigen Betrachtungen muss durch den Punkt P eine Weltlinie w' führen, die parallel zur Achse ct´ verläuft, mit der Neigung tgσ= c/v [ Gleichung (1) ].
Mit steigender Geschwindigkeit v steigt die Steilheit der Weltlinie w´ und der Abstand der Punkte p↔x wird kleiner. Den Abstand p↔x können wir als v.t bezeichnen.
Es handelt sich also um eine Weltlinie deren Lage im Diagram von v abhängt. ( Es wird noch ein mal betont, dass in der physischen Welt beide Systeme S, ´S rechtwinklige Koordinaten haben ).
Die Gleichungen für die Geraden w und w´ haben die Form
(6) w x = c.t ( Senkrechte durch den Punkt P ), und analog für das System S´
(7) w´ w´= x´ = c.t´
Im System S ist die Lage des Punktes p von der Strecke v.t abhänging. Die Weltlinie w´ wird in das System S abgebildet ( transformiert ) als Weltlinie die durch den Punkt p = x-vt führt
(8) w w = ( x - vt ).
Zwischen den Weltlinien w und w´ besteht ein Zusammenhang, den wir als α bezeichnen
(9) w / w´ = ( x - vt) / x´= α -----------------> α. x´ = x - vt
Die Gleichwertigkeit der Systeme S und S´ ( Prinzip der Relativität ) führt zur formal der selben Gleichung
(10) α. x = x´ + vt´ aber v negatives Vorzeichen hat, weil v gegen c für ein aus dem Punkt B´ zum Punkt F´ sich bewegendes Photon, orientiert ist.
Aus den Gleichungen (9) und (10, 12) kann man die Werte x´ und t´ berechnen, falls die Konstante α bekannt ist,
die den Bezug, nur von der Lichtgeschwindigkeit zur Relativen Geschwindigkeit zwischen beiden Systemen darstellen muss. So muss gelten
α = w/w´= x/x´ = ct/ct´.
Gleichsetzung beider Gleichungen (9) x´= (10) x´ führt zur Bestimmung von αt´
(11) (x - vt)/α = α.x - vt´
-v.α.t´= ( x - vt ) - α².x mulipliziert durch ( -1/vα ) ergibt
v.t´= α.x - ( x-v.t ) / α ----------> αt´= α² .x - ( x/v ) + t mit ein Paar Schritten erhält diese Gleichung die Form
(12) α.t´= (x/v) . ( α² - 1 ) + t
Um den Bezug von c und v bestimmen zu können, bietet sich Ersetzung von x und x´ in den Gleichungen (9) und (10) durch c und v. Hierzu verwenden wir die Gleichungen (6) und (7)
(9a) αct´= ct - vt = ( c - v ) . t
(10a) αct = ct´+ vt´= ( c + v ) . t´
Die rechte Seite der Gleichungen bietet durch Multiplikation das bekante Ergebnis (c+v) . (c-v) = (c² - v²). Durch das Multiplizieren der gleichungen miteinander erhält man
(13) α². c² . t . t´ = ( c - v ) . ( c + v ) . t . t´ ----------------> α² = ( c² - v² ) / c² = 1 - (v/c)² ********************************************************************
_____________________________________________________________________________________________________________________________________________________
Literatur
Max Born: Die Relativitätstheorie Einsteins, Springer-Verlag 1984, Franz Embacher, Universität Wien: Lorenz-Transformation ( Home Page ), B.Szallies: Lorenz-Transformation ( Home Page )
Copyright Delektron Datensysteme T.u.H. GmbH 2008, München Germany